Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Descriptive Statements:
- Analyze a variety of patterns.
- Analyze the properties of relations and functions in multiple representations (e.g., tables, graphs, equations, words).
- Analyze direct and inverse proportional relationships.
- Determine the effects of transformations on the graph of a function or relation.
Sample Item:
A hiker climbs uphill at a steady pace, rests at a scenic spot for a while, then continues at a slower pace
to the top of the hill. The hiker stops for lunch at the top, then decides to run down to the base of the hill.
Which of the following graphs best expresses the hiker's speed as a function of time?
Each response is a line graph with the vertical axis labeled Speed and the horizontal axis labeled Time. There are no values marked.
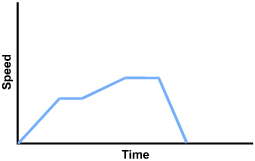 The first segment starts at the origin and slopes up to about a third the height of the vertical axis. The second segment is horizontal, for about half the horizontal distance of the first segment. The third segment slopes up less steeply than the first for about half the vertical distance of the first segment. The fourth segment is horizontal, and is a little longer than the previous horizontal segment. The fifth segment slopes steeply back to the horizontal axis.
The first segment starts at the origin and slopes up to about a third the height of the vertical axis. The second segment is horizontal, for about half the horizontal distance of the first segment. The third segment slopes up less steeply than the first for about half the vertical distance of the first segment. The fourth segment is horizontal, and is a little longer than the previous horizontal segment. The fifth segment slopes steeply back to the horizontal axis.
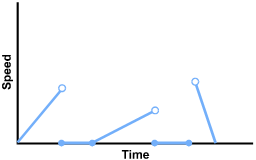 The first segment starts at the origin and slopes up to about a third the height of the vertical axis, ending with an open point. The second segment lies on the horizontal axis for about half the horizontal distance of the first segment, starting and ending with closed points. The third segment begins at the endpoint of the previous segment and slopes up less steeply than the first for about half the vertical distance of the first segment, ending with an open point. The fourth segment lies on the horizontal axis and is a little longer than the previous horizontal segment, starting and ending with closed points. The fifth segment starts with an open point at about the height of the endpoint of the first segment and slopes steeply back to the horizontal axis.
The first segment starts at the origin and slopes up to about a third the height of the vertical axis, ending with an open point. The second segment lies on the horizontal axis for about half the horizontal distance of the first segment, starting and ending with closed points. The third segment begins at the endpoint of the previous segment and slopes up less steeply than the first for about half the vertical distance of the first segment, ending with an open point. The fourth segment lies on the horizontal axis and is a little longer than the previous horizontal segment, starting and ending with closed points. The fifth segment starts with an open point at about the height of the endpoint of the first segment and slopes steeply back to the horizontal axis.
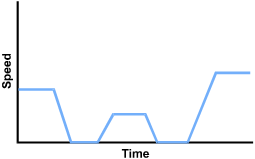 The first segment is horizontal, starting at about a third of the height of the vertical axis. It slopes steeply down to the horizontal axis for a horizontal segment a little shorter than the first horizontal segment. It slopes steeply to a third horizontal segment at about half the height of the first horizontal segment and a little shorter than the first. It slopes steeply down to another horizontal segment on the horizontal axis about the same length as the previous horizontal segment. It slopes steeply up to a horizontal segment about the same length as the first segment, at about half the height of the vertical axis.
The first segment is horizontal, starting at about a third of the height of the vertical axis. It slopes steeply down to the horizontal axis for a horizontal segment a little shorter than the first horizontal segment. It slopes steeply to a third horizontal segment at about half the height of the first horizontal segment and a little shorter than the first. It slopes steeply down to another horizontal segment on the horizontal axis about the same length as the previous horizontal segment. It slopes steeply up to a horizontal segment about the same length as the first segment, at about half the height of the vertical axis.
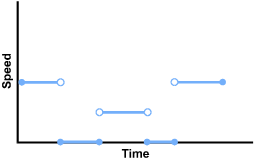 The first is at about 40% of the height of the vertical axis, starting with a closed point and ending with an open point. The second is on the horizontal axis, about the same length as the first, starting and ending with closed points. The third is about half the height of the first and a little longer, starting and ending with open points. The fourth is on the horizontal axis, shorter than the first, starting and ending with closed points. The fifth is at the same height as the first and about as long as the third, starting with an open point and ending with a closed point.
The first is at about 40% of the height of the vertical axis, starting with a closed point and ending with an open point. The second is on the horizontal axis, about the same length as the first, starting and ending with closed points. The third is about half the height of the first and a little longer, starting and ending with open points. The fourth is on the horizontal axis, shorter than the first, starting and ending with closed points. The fifth is at the same height as the first and about as long as the third, starting with an open point and ending with a closed point.
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
C. This question requires the examinee to analyze the properties of relations and
functions in multiple representations (e.g., tables, graphs, equations, words). The "steady pace" held
by the hiker reflects a constant speed over time; thus the first section of the graph is a horizontal line
(slope equals zero) at some constant value of speed. The hiker slows to a resting position with a speed
of zero, though time passes so the value for time continues to increase. The approach to the top of the hill
shows a positive slope, with increasing speed and time as the hiker resumes walking, but since the pace is
slower, the graph does not reach the previous level of speed. This pattern repeats when the hiker stops
for lunch, but the run to the base reflects a greater speed than was achieved on the initial climb.
Descriptive Statements:
- Manipulate algebraic expressions, equations, and inequalities (e.g., simplify, transform, factor).
- Solve linear and nonlinear equations and inequalities.
- Connect appropriate algebraic notation to phrases and sentences.
Sample Item:
If a person can buy up to 3 times as many desktop computers as laptop computers with the same amount
of money, then which of the following inequalities relates the price of a desktop computer D to the
price of a laptop computer L?
- D ≤ 3LD is less than or equal to 3L
- D ≥ 3LD is greater than or equal to 3L
- 3D ≤ L3D is less than or equal to L
- 3D ≥ L3D is greater than or equal to L
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
D. This question requires the examinee to connect appropriate algebraic notation to phrases and sentences. The condition of "up to 3 times as many" is the same as 1 laptop computer having the value of at most 3 desktop computers. Thus for the price of a desktop computer, D, and the price of a laptop computer, L, 3D ≥ L3D is greater than or equal to L.
Descriptive Statements:
- Analyze the relationship between a linear equation or inequality and its representations.
- Solve systems of linear inequalities or equations with a variety of methods.
- Interpret the meaning of the slope and the y-intercept in various contexts.
- Analyze a variety of real-world problems involving linear equations, systems, and inequalities.
Sample Item:
Which of the following is an equation of a line perpendicular to the line 4x – 9y = 124x minus 9y equals 12?
- y = 9/4x + 6y equals 9 fourths x plus 6
- y = 4/9x + 3y equals 4 ninths x plus 3
- y = – 4/9x − 4y equals negative 4 ninths x minus 4
- y = – 9/4x − 2y equals negative 9 fourths x minus 2
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
D. This question requires the examinee to analyze the relationship between a
linear equation or inequality and its representations. The slope, m1, of the given line is found by isolating y in the given equation. 4x − 9y = 12 ⇒ 9y = 4x − 12 ⇒ y = 4/9x − 12/9 and m1 = 4/94x minus 9y equals 12 which becomes 9y equals 4x minus 12 which becomes y equals 4 ninths x minus 12 ninths and m1 equals 4 ninths. The slope, m⊥m perpendicular, of a line perpendicular to the given line is the negative reciprocal of the slope of the given line m1. Thus m⊥ = – 1/m1 so m⊥ = – 9/4 and y = – 9/4x − 2m perpendicular equals negative 1 over m1 so mperpendicular equals negative 9 fourths and y = negative 9 fourths x minus 2 must be the equation of the perpendicular line.
Descriptive Statements:
- Analyze relationships between multiple representations of a nonlinear equation or inequality.
- Solve a variety of real-world problems involving nonlinear equations and inequalities.
- Analyze function behavior in terms of limits, continuity, and rates of change.
- Apply concepts of calculus to solve problems in real-world situations.
Sample Item:
If the limit of function h(x)h of x equals a real number k as x goes to negative infinity, which of the
following is the equation of an asymptote of the graph of h(x)h of x?
- x = –kx equals negative k
- y = –ky equals negative k
- x = kx equals k
- y = ky equals k
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
D. This question requires the examinee to analyze function behavior in terms of limits, continuity, and rates of change. The situation described can be represented as 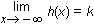 the limit as x approaches negative infinity of h of x equals k. This means that as x approaches negative infinity, h(x)h of x approaches but never reaches k and that y = ky equals k is a horizontal asymptote.
the limit as x approaches negative infinity of h of x equals k. This means that as x approaches negative infinity, h(x)h of x approaches but never reaches k and that y = ky equals k is a horizontal asymptote.

